In parallel with the optimization of crane pads (you can find the article on the topic here) I am also trying to automate the calculation of wind farm internal roads.
At the moment I have developed three solutions: the first joins the turbines looking for the minimum spanning tree (MST), i.e., the shortest possible connection.
I would say that this solution can make sense in those wind farms in flat desert areas, where we have hundreds of hectares with no natural, orographic or constraints to consider. I have worked on some parks that have these characteristics, for example, those located in desert areas in southwestern Morocco.
A second solution complements the MST’s research with the use of existing roads and considers areas where we cannot access (for example, because we have not acquired the rights, or because of environmental constraints).
In this case, the problem is solved by considering that sections of existing road have zero cost (because the road has already been built). To avoid “no go areas,” on the other hand, sera’ necessary to use a series of auxiliary points that will allow for alternative undirected routes.
Finally, we have the third case, where we want to consider existing orography.
It is necessary to work with a digital terrain model (usually in .tif format).
The solution implemented creates a mesh of points with regular spacing.
Subsequently, each point is joined with the 8 points surrounding it creating a network with several thousand links.
For each pair of points, the slope (basically the difference in elevation between the two points divided by the distance) is calculated.
The next step is to penalize the connections with the steepest slope – that is, we want to avoid carrying nacelles on sections with steep slopes. In addition, sections in mountainous areas usually have greater earth movements than sections built in flat areas.
The algorithm will then consider 100 meters flat as “cheaper” than 100 meters with a 6% slope, which in turn will be cheaper than 100 meters with a 12% slope.
In the final step, the cheapest solution to join the turbines together is found.
How long does it take to find the result?
Complexity increases rapidly with the number of auxiliary points we want to consider. For example, if we decide to have a mesh with points every 100 meters in a square kilometer we will have 100 points-but if we want points every 50 meters in the same square kilometer we will have 400.
The number of connections between points (“edges”) also increases, of course. And it is precisely in calculating the cost of edges that the algorithm takes a significant amount of time.
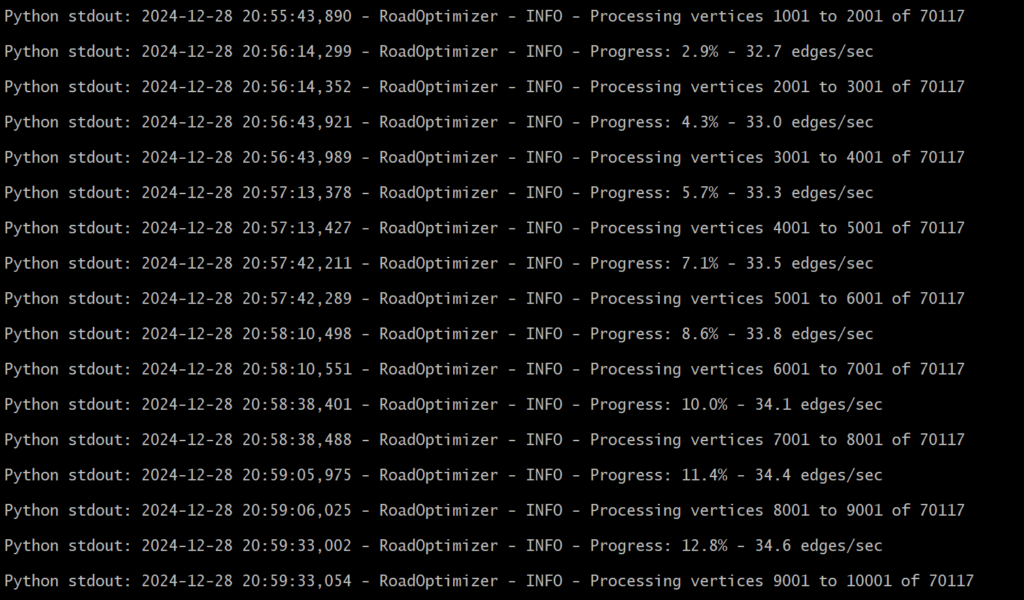
My server calculates the cost of 35 to 45 edges per second. I guess it is possible to increase the speed, for example with a multithreading solution.
I will try to experiment in the coming days.
Leave a Reply